Image:
 Author: s_noonan Group: Technical Filesize: 21.4 kB Date added: 2017-02-17 Rating: 5 Downloads: 617 Views: 431 Comments: 6 Ratings: 1 Times favored: 0 Made with: Algodoo v2.1.0 Tags:
|
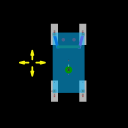
The intention of this scene is to show a different method for coding wheel friction. It is not intended to be an improvement over The Linkages scene.
up/down for accelerator/brake. left/right for steering.
Notes:
1. This scene is written from the tire's point of view.
2. The code in all the tires is the same.
3. The only difference in the tires is that some have _driven = true and some have _driven = false.
4. This rear wheel drive car can be converted to a front wheel drive or 4 wheel drive by changing the tires' _driven properties.
5. The speed setting knob acts as accelerator and brake.
6. _maxPower in the speed setting knob hinge determines the engine max power.
7. This scene does not use Kilinich's K-Wheels.
8. u and v are the tire's local x and y coordinate system.
9. The code takes into account the angle of the friction force when braking.
10. The code assumes that tire side friction is 10% of the friction force when "peeling out". This is because the relative velocity between the spinning tire and the road is unknown.
11. Tires turn red when slipping.
Rev A: Steering returns to center when released. |
Last edited at 2017/03/12 11:54:27 by s_noonan
Please log in to rate this scene |




.png)