Ekvationsvåg
From Algodoo
(Difference between revisions)
Bjorn.enare (Talk | contribs) (Skapade sidan med '{{Lesson |language=lesson-swedish |title=Ekvationsvåg |description=En modell av en våg som kan användas för att visa hur den så kallade "balansmetoden" fungerar vid ekvation...') |
|||
| Line 5: | Line 5: | ||
|target=lesson-keystage2, lesson-keystage3, lesson-keystage4 | |target=lesson-keystage2, lesson-keystage3, lesson-keystage4 | ||
|type=lesson-demonstration, lesson-exercise | |type=lesson-demonstration, lesson-exercise | ||
| - | |keywords=lesson-static-forces | + | |keywords=lesson-static-forces |
|objectives=Ur lgr 11. Centralt innehåll i matematik. | |objectives=Ur lgr 11. Centralt innehåll i matematik. | ||
| Line 13: | Line 13: | ||
åk 7-9 | åk 7-9 | ||
"Metoder för ekvationslösning." | "Metoder för ekvationslösning." | ||
| - | |inclass=Skriv en lämplig ekvation på tavlan och lös den. | + | |inclass=Skriv en lämplig ekvation på tavlan och lös den. Visa samtidigt hur ekvationen löses i modellen. Balansen bibehålls genom att värdet minskas på båda sidor av vågen. |
| + | Modellen tillåter inte lösning av ekvationer där konstanterna är negativa. | ||
| + | Exempelvis 3x - 4 = 5 blir svårt eftersom -4 då motsvarar en "lyftkraft" 40 N i VL. | ||
| + | Denna begränsning kan dock vara en ingång till diskussion med eleverna om varför matematiska samband inte alltid kan visas på ett konkret sätt, utan måste gå över i abstrakt form för att bli meningsfull. | ||
}} | }} | ||
{{StartScenes}} | {{StartScenes}} | ||
| Line 42: | Line 45: | ||
|text=Modellen tillåter inte lösning av ekvationer där konstanterna är negativa. | |text=Modellen tillåter inte lösning av ekvationer där konstanterna är negativa. | ||
Exempelvis 3x - 4 = 5 blir svårt eftersom -4 då motsvarar en "lyftkraft" 40 N i VL. | Exempelvis 3x - 4 = 5 blir svårt eftersom -4 då motsvarar en "lyftkraft" 40 N i VL. | ||
| - | |||
}} | }} | ||
{{EndInAlgodoo}} | {{EndInAlgodoo}} | ||
Latest revision as of 12:45, 8 May 2014
Ekvationsvåg
| Language: | Svenska |
|---|---|
| Description: | En modell av en våg som kan användas för att visa hur den så kallade "balansmetoden" fungerar vid ekvationslösning. |
| Target: | Key Stage 2, Key Stage 3, Key Stage 4 |
| Category: | Demonstration, Exercise |
| Discipline: | Static forces |
| Learning objectives: |
Ur lgr 11. Centralt innehåll i matematik. åk 4-6 "Metoder för enkel ekvationslösning." åk 7-9 "Metoder för ekvationslösning." |
| In class: | Skriv en lämplig ekvation på tavlan och lös den. Visa samtidigt hur ekvationen löses i modellen. Balansen bibehålls genom att värdet minskas på båda sidor av vågen.
Modellen tillåter inte lösning av ekvationer där konstanterna är negativa. Exempelvis 3x - 4 = 5 blir svårt eftersom -4 då motsvarar en "lyftkraft" 40 N i VL. Denna begränsning kan dock vara en ingång till diskussion med eleverna om varför matematiska samband inte alltid kan visas på ett konkret sätt, utan måste gå över i abstrakt form för att bli meningsfull. |
Steps in Algodoo
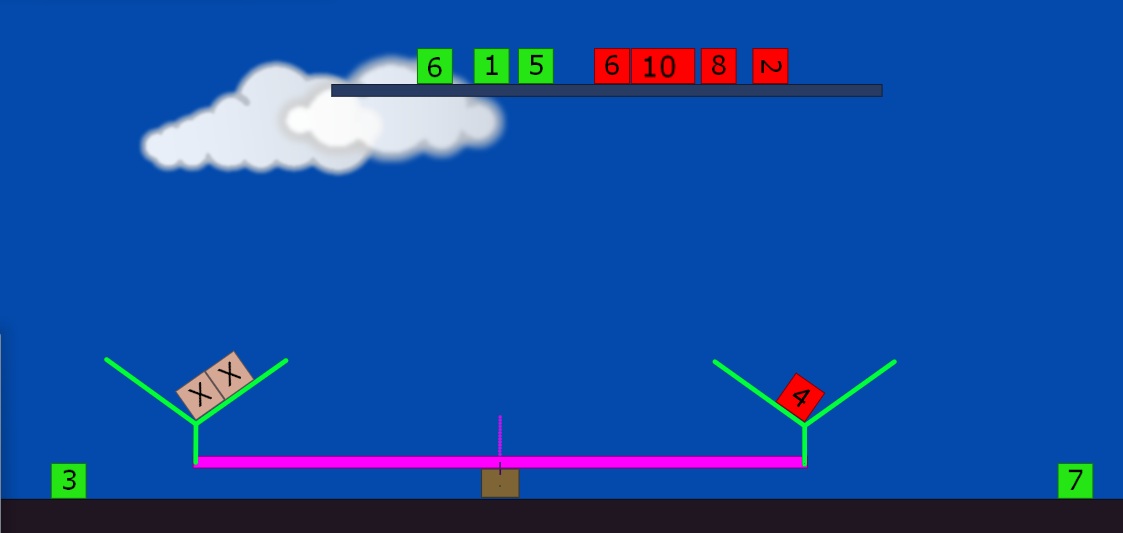
Lös ekvationen 2x+3=7
När simulationen startas råder jämvikt på vågen. Plocka bort "trean" från VL och minska samtidigt HL med tre, byt ut "sjuan" mot en "fyra".
Ekvationen är nu 2x = 4.
Dela med VL o HL med 2 för att få x=2.
Minska med 3 i VL och HL, kontrollera att balansen bibehålls.
Gör egna ekvationer
Rektanglarna med tal har en massa som motsvarar talets värde. "Ettan" har massan 1 kg, "tvåan" 2 kg, osv.
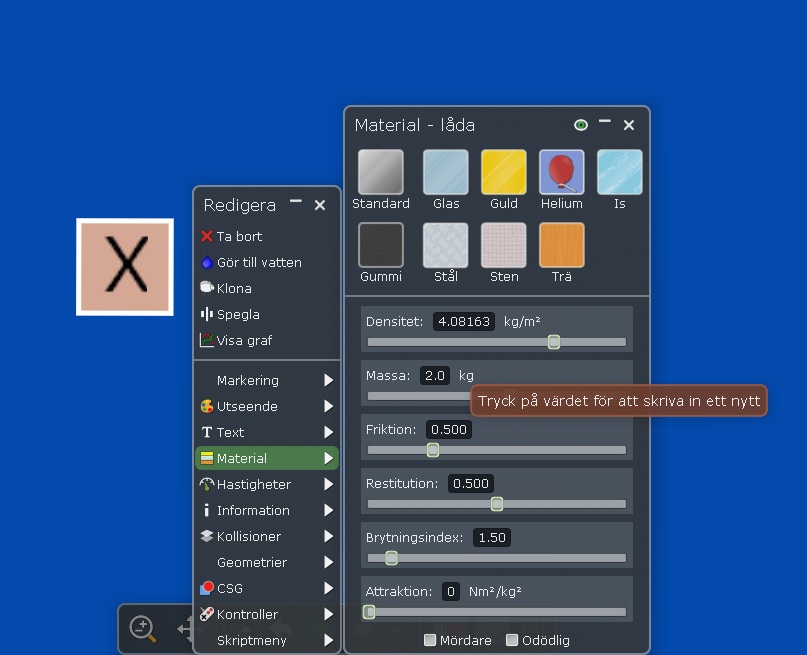
Variabeln X har i modellen massan 2 kg. Detta kan lätt ändras genom att höger klicka på "X" och under "material" ändra till önskad massa.
Om det önskas tal som är större än 10, använd klon funktionen. Byt sedan text och massa på samma sätt som för "X".
Höger klicka på "X" och ändra till önskad massa för att kunna göra nya ekvationer.
Begränsningar
Modellen tillåter inte lösning av ekvationer där konstanterna är negativa.
Exempelvis 3x - 4 = 5 blir svårt eftersom -4 då motsvarar en "lyftkraft" 40 N i VL.
