Image:
 Author: FRA32 Group: Default Filesize: 511.63 kB Date added: 2018-12-01 Rating: 6.5 Downloads: 4630 Views: 920 Comments: 4 Ratings: 4 Times favored: 0 Made with: Algodoo v2.1.0 Tags:
|
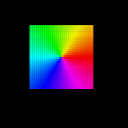
This scene shows how the so called "Newton Fractal" is calculated.
A grid of points between -1,-1 and 1,1 (Complex number plane) is put into the function x^3-1. Then the so called Newton Method is applied.
The Newton method takes a point and moves it according to it's proximity to a root and the direction of the derivative. This almost always ends up with the point wandering into the general direction of a root and then sticking to it. However, the position of the initial point greatly determines at which root it ends up. In this example, there are 3 roots, but a point can only arrive at one of them. Depending on which root it reaches, the original point will be colored according to the coordinate of the root(Complex domain coloring method).
In this scene, the grid of points will follow Newtons method a total of 15 times, moving to the new point every time. After 15 steps, they will take on the color of their current coordinate and return to their original position, revealing the points that arrive at each root. At the same time, a high definition picture of the result will be shown for comparison.
The final result is a unique fractal, consisting of 3 great areas, whose edges consist of smaller version of the third area each, which then again has replicas of the other areas at it's edges. At every single point of this complex edge, all 3 colors touch. |