2重振子
From Algodoo
(Difference between revisions)
| (2 intermediate revisions not shown) | |||
| Line 12: | Line 12: | ||
|inclass=(1) 微小振動の近似を用いて運動方程式を立てましょう | |inclass=(1) 微小振動の近似を用いて運動方程式を立てましょう | ||
(2) モード(規準振動)の振動数すなわち固有振動数を求めましょう | (2) モード(規準振動)の振動数すなわち固有振動数を求めましょう | ||
| + | |||
(3) モードの重ね合わせによって一般解を求めましょう | (3) モードの重ね合わせによって一般解を求めましょう | ||
| + | |||
(4) シミュレーションで一般解を検証しましょう | (4) シミュレーションで一般解を検証しましょう | ||
}} | }} | ||
{{StartScenes}} | {{StartScenes}} | ||
| - | {{Scene}} | + | {{Scene |
| + | |scene=58962 | ||
| + | }} | ||
{{EndScenes}} | {{EndScenes}} | ||
{{StartInAlgodoo}} | {{StartInAlgodoo}} | ||
| Line 22: | Line 26: | ||
|headline=(1) 微小振動の近似を用いて運動方程式を立てましょう | |headline=(1) 微小振動の近似を用いて運動方程式を立てましょう | ||
|text=ラグランジアンをつくって微分により運動方程式を立てましょう。 | |text=ラグランジアンをつくって微分により運動方程式を立てましょう。 | ||
| + | |||
| + | |||
http://www14.atwiki.jp/yokkun/pages/285.html | http://www14.atwiki.jp/yokkun/pages/285.html | ||
|image=WPend1.PNG | |image=WPend1.PNG | ||
Latest revision as of 01:53, 15 November 2011
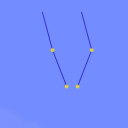
2重振子
| Language: | 日本語 |
|---|---|
| Description: | カオスの入り口ともいうべき2重振子の解析に挑戦します。微小振動の近似をとって,ラグランジアンから運動方程式を立て,系の固有振動数と一般解を導出します。 |
| Target: | Key Stage 6 |
| Category: | Demonstration, Exercise |
| Discipline: | Motion, Energy |
| Learning objectives: |
拘束系の運動解析の簡明な方法としてラグランジアンの微分により運動方程式を立てることができるようにします。モード(規準振動)の重ね合わせによって振動系の一般解が得られることを理解し,シミュレーションによって検証します。 http://www14.atwiki.jp/yokkun/pages/285.html http://www14.atwiki.jp/yokkun/pages/354.html |
| In class: | (1) 微小振動の近似を用いて運動方程式を立てましょう
(2) モード(規準振動)の振動数すなわち固有振動数を求めましょう (3) モードの重ね合わせによって一般解を求めましょう (4) シミュレーションで一般解を検証しましょう |
Steps in Algodoo
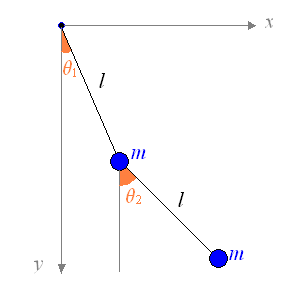
(1) 微小振動の近似を用いて運動方程式を立てましょう
ラグランジアンをつくって微分により運動方程式を立てましょう。
(2) モード(規準振動)の振動数すなわち固有振動数を求めましょう
系全体が同一の振動数と位相で振動する状態をモード(規準振動)といいます。自由度2の2重振子には2つのモードが存在します。2つのモードの振動数すなわち系の固有振動数を求めましょう。
http://www14.atwiki.jp/yokkun/pages/354.html
(3) モードの重ね合わせによって一般解を求めましょう
2つのモードの重ね合わせによって一般解が得られます。
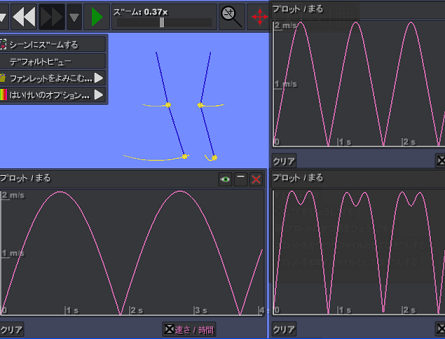
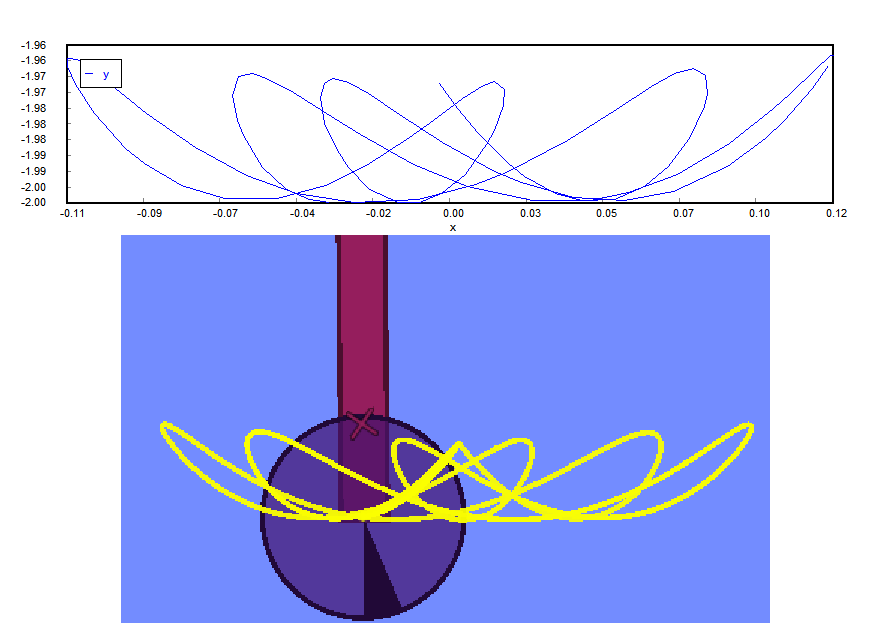
(4) シミュレーションで一般解を検証しましょう
適当な初期条件を設定してAlgodooによってシミュレーションを実行し,一般解を検証しましょう。数値積分ツールがあれば数値積分結果と比較してみましょう。
「物理シミュレータAlgodooで学ぶ力学」
書籍「物理シミュレータAlgodooで学ぶ力学」に2重振子の解析と演習問題を掲載しています。