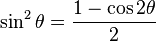mechanical ballistic computer [updated]
16 posts • Page 1 of 1
mechanical ballistic computer [updated]
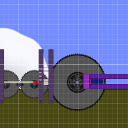
Inspired by conundrumer's ballistic computer, I created this:
here's new one:
Not so sophisticated and not super accurate, but I like simplicity
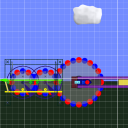
here's new one:
Not so sophisticated and not super accurate, but I like simplicity
Last edited by davidz40 on Thu Oct 22, 2009 6:23 pm, edited 2 times in total.
Phundamentalist
-

davidz40 - Posts: 438
- Joined: Sun Sep 06, 2009 10:30 am
Re: mechanical ballistic computer
If you have a problem with consistent initial velocity then just use a spring bullet. Those always expend a measured amount of energy whereas superbouncy reactions can be more or less powerful depending on the speed that the projectile hits the high restitution surface.

-

Paradigm 29 - Posts: 284
- Joined: Tue Sep 01, 2009 12:06 am
- Location: Houston, Tx
Re: mechanical ballistic computer
actually I use repulsion instead of superbouncy to get better precision, but I'll switch to spring bullet. Thanks for advice. I'm actually trying to measure shot height too, but for now, I don't know how to "calculate" sina*sina (or any other expotentiation)
Phundamentalist
-

davidz40 - Posts: 438
- Joined: Sun Sep 06, 2009 10:30 am
Re: mechanical ballistic computer
davidz40 wrote:[...] I'm actually trying to measure shot height too, but for now, I don't know how to "calculate" sina*sina (or any other expotentiation)
I will deduce the "formula" for you. But first... I have to play Wii Sports Resort

-

KarateBrot - Posts: 825
- Joined: Mon Aug 31, 2009 7:32 pm
- Location: Germany
Re: mechanical ballistic computer
The position function for a falling object is -1/2at^2+Vit or -4.9t^2+Vit.
Since Vi is also a known constant (after you get better bullets) the velocity function for the falling object is -9.8t+Vi.
If you want to get the Y distance then you'll need to use this: -9.8t +Vi*Sin(theta)
Plug in whatever Vi you got and set the equation to 0 (for example say Vi=100 and let (theta)=30 degrees). It should look like:
-9.8t+100Sin(30) = 0 which simplifies to
-9.8t+100*1/2 = 0
-9.8t+50 = 0
9.8t = 50
t=50/9.8
So, if your cannon is pointed 30 degrees above the horizontal and is shot from the cannon at 100m/s, then it will take 50/9.8 seconds (decimal is ~5.1s) for it to reach it's highest point. Now lets go back to the position function!
-4.9t^2 + Vit or -4.9t^2 +100t
which, according to the time it took to get to the highest point (5.1s) is:
-4.9(5.1)^2 + 100(5.1)
= -127.4 + 510
= 382.6
So, your maximum height would be 382.6m
The equation for the maximum height achieved on a projectile curve again is:
y = 1/2*a*{[Vi*Sin(theta)]/a}^2 + (Vi*Sin(theta))*{[Vi*Sin(theta)]/a}
=3(Sin(theta))^2 * Vi^2 / 2a
Wikipedia or some other internet site could maybe give you a method that requires less inputs.
How do you do that mechanically? I don't know. I do know that Conundrumer used a Sine generator which is basically the wood mechanics scene. Really though, it's probably going to be beyond most of us normal people to figure that out by mechanical means.
Since Vi is also a known constant (after you get better bullets) the velocity function for the falling object is -9.8t+Vi.
If you want to get the Y distance then you'll need to use this: -9.8t +Vi*Sin(theta)
Plug in whatever Vi you got and set the equation to 0 (for example say Vi=100 and let (theta)=30 degrees). It should look like:
-9.8t+100Sin(30) = 0 which simplifies to
-9.8t+100*1/2 = 0
-9.8t+50 = 0
9.8t = 50
t=50/9.8
So, if your cannon is pointed 30 degrees above the horizontal and is shot from the cannon at 100m/s, then it will take 50/9.8 seconds (decimal is ~5.1s) for it to reach it's highest point. Now lets go back to the position function!
-4.9t^2 + Vit or -4.9t^2 +100t
which, according to the time it took to get to the highest point (5.1s) is:
-4.9(5.1)^2 + 100(5.1)
= -127.4 + 510
= 382.6
So, your maximum height would be 382.6m
The equation for the maximum height achieved on a projectile curve again is:
y = 1/2*a*{[Vi*Sin(theta)]/a}^2 + (Vi*Sin(theta))*{[Vi*Sin(theta)]/a}
=3(Sin(theta))^2 * Vi^2 / 2a
Wikipedia or some other internet site could maybe give you a method that requires less inputs.
How do you do that mechanically? I don't know. I do know that Conundrumer used a Sine generator which is basically the wood mechanics scene. Really though, it's probably going to be beyond most of us normal people to figure that out by mechanical means.
Last edited by Paradigm 29 on Thu Oct 22, 2009 4:40 pm, edited 1 time in total.

-

Paradigm 29 - Posts: 284
- Joined: Tue Sep 01, 2009 12:06 am
- Location: Houston, Tx
Re: mechanical ballistic computer
Paradigm 29 wrote:How do you do that mechanically? I don't know. I do know that Conundrumer used a Sine generator which is basically the wood mechanics scene. Really though, it's probably going to be beyond most of us normal people to figure that out by mechanical means.
i would say he wants it mechanically because he knows the function for the trajectory parabola, i guess, because he calculated the maximum distance with it. and he also said he doesn't know how to do an expotentiation with sin²a. the formula for the maximum height includes sin² so i think he knows the formula which is y = v²sin²α / (2g) by the way.

-

KarateBrot - Posts: 825
- Joined: Mon Aug 31, 2009 7:32 pm
- Location: Germany
Re: mechanical ballistic computer
ah, sorry, well. Perhaps you could use 2 Sine generators whose outputs are connected to an analog multiplier?

-

Paradigm 29 - Posts: 284
- Joined: Tue Sep 01, 2009 12:06 am
- Location: Houston, Tx
Re: mechanical ballistic computer
Last edited by Conundrumer on Thu Oct 22, 2009 4:29 am, edited 1 time in total.
-

Conundrumer - Posts: 344
- Joined: Mon Aug 31, 2009 5:55 pm
- Location: NYC
Re: mechanical ballistic computer
Conundrumer wrote:
QED
that's the formula my ideas are based on
but there's a probability of i would say 70% that i will fail
[EDIT]
There you go
Does this example help you with sin² ?

-

KarateBrot - Posts: 825
- Joined: Mon Aug 31, 2009 7:32 pm
- Location: Germany
Re: mechanical ballistic computer
I didn't expect so much feedback 
Example helped me a lot, I totally forgot that sin2 can be trasformed such way that no expotention is needed .
.
Now I'm going to create ultra-complicated mechanism that takes air friction into account lol
BTW what's the advantage of c-gears over standard ones?
Example helped me a lot, I totally forgot that sin2 can be trasformed such way that no expotention is needed
Now I'm going to create ultra-complicated mechanism that takes air friction into account lol
BTW what's the advantage of c-gears over standard ones?
Phundamentalist
-

davidz40 - Posts: 438
- Joined: Sun Sep 06, 2009 10:30 am
Re: mechanical ballistic computer
C-gears always have constant contact. That means they are less likely to slip under large amounts of torque and are more accurate than the default gears.

-

Paradigm 29 - Posts: 284
- Joined: Tue Sep 01, 2009 12:06 am
- Location: Houston, Tx
Re: mechanical ballistic computer
Phundamentalist
-

davidz40 - Posts: 438
- Joined: Sun Sep 06, 2009 10:30 am
Re: mechanical ballistic computer [updated]
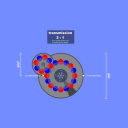
wow nice
and its far smaller than con´s
and its far smaller than con´s
I AM Phundamentalist
Newest Scene
Newest Scene
-

Tank2333 - Posts: 105
- Joined: Tue Sep 01, 2009 12:52 am
- Location: Old PhunLand
Re: mechanical ballistic computer
davidz40 wrote:Now I'm going to create ultra-complicated mechanism that takes air friction into account lol
holy **** this would be an incredible complicated and complex mechanism. if you success you're god

-

KarateBrot - Posts: 825
- Joined: Mon Aug 31, 2009 7:32 pm
- Location: Germany
16 posts • Page 1 of 1
Who is online
Users browsing this forum: No registered users and 7 guests